
Step 2: From the second equation, find the same unknown quantity of values in relation to the other equations. Step 1: From the first equation, find an unknown quantity of values in relation to other equations.

Insert this value into one of the two given equations to find the other unknown value. Step 3: Solve the resulting equation to find one value of the unknown.

All that remains is either the x or y only equation. Step 2: Add or subtract one equation to the other so that terms with the same numeric coefficients cancel each other out. Step 1: Multiply one or both equations by one or more appropriate numbers so that either the x or y coefficients of both equations are numerically the same. And this way you find the values of all the unknown variables.

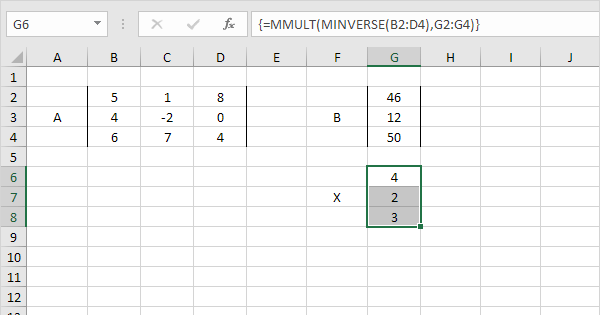
Step 3: Substituting the value of the variable obtained in step 2 above will result in the results of step 1 getting the values of the remaining unknown variable. Step 2: Substitute the value of the variable obtained in step 1 above into another equation and solve it to get the value of one variable. Step 1: From the two equations given, consider one of the equations from the question and then find the value of one variable in relation to another variable. There are three common methods in which you can solve the Simultaneous Equations in the method that is apt for the question and sometimes it may not be the one you prefer but you still got to do it. Methods of Solving Simultaneous Equations Thus, the two equations x - y= 2, x + y= 8 will both be satisfied by the same pair of values of x and y only when x= 5 and y= 3. However, if, together with this equation we consider the equation x + y= 8 then x and y must be such that their difference is 2 and their sum is 8. There are an infinite number of solutions to this equation, as every pair of numbers with a difference of 2 satisfies the equation. Let us consider the equation x - y = 2, where both x and y are unknown. They are called Simultaneous Equations because the equations are solved together at the same time. Simultaneous Equations are two equations, each with the same two unknowns, and require algebraic skills to find the character values of two or more equations. They can set different Mathematical expressions to align with different goals, like running the farthest distance, building endurance, or maximize speed. Athletes and cyclists can use the three key variables of speed, distance, and time to calculate the best routes for their daily practice regimen. Accountants, auditors, budget analysts, Insurance underwriters, and loan officers use equations to balance accounts, determine the pricing, and to set budgets. Real-life Applications of Simultaneous Equationsįinancial fields often require the use of linear equations. The different types of Mathematical equations are- linear, quadratic, and polynomial. When values are substituted, there has to be equality. The LHS and the RHS have to be (=) equal. There are two sides to an expression or equation. As you know, equations are algebraic expressions. When we study Maths, we understand that an equation is a statement in which two things are equal. To solve the equations, we need to find the values of the variables that are part of these equations.
T o work on thes e means looking out for the standard solution. It is the reason why Simultaneous Equations are also known as the system of equations, in which it consists of a finite set of equations. It is an essential point to remember that these equations include a set of few independent equations. Simultaneous Equations need algebraic skills to find the values of letters within two or more equations. They are Simultaneous Equations because the equations are solved at the same time. When you are asked to solve such equations, you must find values of the unknowns which satisfy all the given equations at the same time. There are times when you come across two or more unknown quantities and two or more equations relating to them. Simultaneous Equation is an essential Chapter in the Algebra branch of Mathematics.


 0 kommentar(er)
0 kommentar(er)
